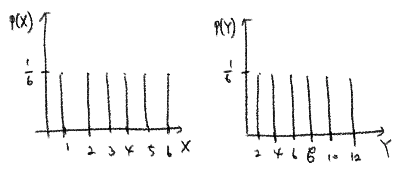
확률변수의 기댓값
- 기댓값(expectation)
- 확률변수의 확률밀도함수를 통해 얻은 확률변수의 이론적 평균값 (= 평균)
- \(E[X]\) (\(X\): 확률변수)
- \(\mu_X\) or \(\mu\)
- 이산확률변수의 기댓값
- 표본공간의 원소 \(x_i\)의 가중평균
- \(\mu_X\) \(= E[X]\) \(= \sum_{x_i \in \Omega} x_ip(x_i)\)
- e.g. 주사위
- \[\mu_X = 1 \cdot p(1) + 2 \cdot p(2) + 3 \cdot p(3) + 4 \cdot p(4) + 5 \cdot p(5) + 6 \cdot p(6) = {7 \over 2}\]
- 표본평균
- \[\bar x = {1 \over N} \sum^N_{i=1}x_i\]
- 기댓값 공식에서 \(x_i\)는 표본공간의 모든 원소를 뜻하지만 표본평균 공식에서 \(x_i\)는 선택된(sampled, realized) 표본만을 뜻함
- 연속확률변수의 기댓값
- 확률밀도함수를 가중치로 하여 모든 가능한 표본을 적분한 값
- \[\mu_X = E[ X ] = \int^{\infty}_{-\infty}xp(x)dx\]
- 기댓값은 여러 가능한 값을 확률(또는 확률밀도)값에 따라 가중합을 한 것이므로 가장 확률(또는 확률밀도)이 높은 값 근처의 값이 됨
확률변수의 변환
- 기존의 확률변수를 사용하여 새로운 확률변수를 만드는 것
- \[Y = f(X)\]
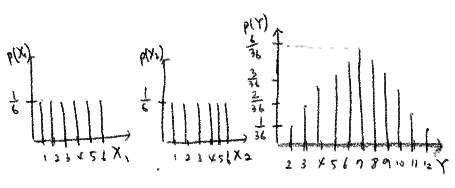
- 여러 확률변수가 있을 때도 성립 (\(Z = X + Y\))
- 확률변수에서 표본을 N번 뽑아서 그 값을 더하는 경우
- \[Y = X_1 + X_2 + \cdots + X_N\]
- \(X_1\)과 \(X_2\)가 같은 확률분포를 가지는 확률변수이지만 표본값이 다르기 때문에 \(Y = X + X + \cdots + X\)는 전혀 다름
기댓값의 성질
- \(E[c] = c\) (\(c\): 확률변수가 아닌 상수)
- \[E[cX] = cE[X]\]
- \(E[X+Y]\) \(= E[X]\) \(+ E[Y]\)
- \(E[c_1X + c_2Y]\) \(= c_1E[X]\) \(+ c_2E[Y]\)
통계량(statistics)
- 확률변수 X로부터 데이터 집합 {\(x_1, x_2, \cdots, x_N\)}을 얻었을 때, 데이터 집합의 모든 값을 정해진 공식에 넣어서 하나의 숫자로 구한 것
- ex) 표본의 합, 표본평균, 표본중앙값, 표본분산 등
- 통계량도 확률변수의 변환에 포함
표본평균 확률변수
- 확률변수로부터 N개의 표본을 만들어 구한 집합의 평균 값
- \[\bar X\]
-
\[\bar X = {1 \over N} \sum_{i=1}^N X_i\]
- \(X_i\): i번째로 실현된 표본값을 생성하는 확률변수, 원래 확률변수 X의 복사본
기댓값과 표본평균의 관계
- \(E[\bar X] = E[X]\)
(증명)
\(E[\bar X] = E[{1 \over N} \sum_{i=1}^N X_i] = {1 \over N} \sum_{i=1}^NE[X_i]\)
\(= {1 \over N} \sum_{i=1}^N\) \(E[X]\) \(= {1 \over N} N\) \(E[X]\) \(= E[X]\)
\(\rightarrow\) 표본평균은 확률변수의 기댓값 근처의 값이 된다
중앙값
- 확률변수의 중앙값(median): 중앙값보다 큰 값이 나올 확률과 작은 값이 나올 확률이 0.5로 같은 값
- \(F(x)\): 누적확률분포, \(0.5 = F(\) 중앙값 \()\) \(\leftrightarrow\) 중앙값 = \(F^{-1}(0.5)\)
최빈값
- 이산확률분포에서는 가장 확률 값이 큰 수
- 연속확률분포에서는 확률밀도함수 \(p(x)\)의 값이 가장 큰 확률변수의 값 (= 확률밀도함수의 최댓값)
- 최빈값 = \(\arg \max_x p(x)\)
연습문제
- 7.2.1
- \(E[X]\) \(= 1 \cdot p(1) + 0 \cdot p(0) = {1 \over 2}\)
- 7.2.3
- \[E[ Y ] = {1 \over 2} \times 180 \times 0.35 + {1 \over 2} \times 180 \times (0.35 + 0.175) = 78.75\]
- 7.2.4
- 7.2.5
- 7.2.6
- 표본 분산도 확률적인 데이터이다
- \[s^2 = {1 \over N} \sum^N_{i=1} (X_i- \bar X)^2 = {1 \over N} \sum^N_{i=1} (X_i- {1 \over N} \sum^N_{i=1} X_i)^2\]
이 글은 ‘데이터 사이언스 스쿨 수학편’을 정리한 것입니다.
질문이나 오류가 있다면 댓글 남겨주세요.