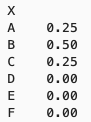
결합확률질량함수
- 결합확률질량함수 (joint probability mass function)
- 특정한 숫자 쌍인 경우, 각각의 사건에 대해서 확률질량함수가 있으면 전체 확률분포를 알 수 있음
- \[p_{XY}(x, y)\]
주변확률질량함수
- 주변확률질량함수 (marginal probability mass function)
- 두 확률변수 중 하나의 확률변수 값에 대해서만 확률분포를 표시한 함수
= 다변수가 되기 이전의 단변수 확률질량함수 - 결합확률질량함수에서 주변확률질량함수은 다른 변수가 가질 수 있는 모든 값의 결합확률질량함수를 합한 확률
- \[p_X(x) = \sum_{y_i} p_{XY}(x, y_i)\]
- \[p_Y(y) = \sum_{x_i} p_{XY}(x_i, y)\]
- 두 확률변수 중 하나의 확률변수 값에 대해서만 확률분포를 표시한 함수
조건부확률질량함수
- 조건부확률질량함수 (conditional probability mass function)
- 다변수 확률변수 중 하나의 값이 고정되어 있을 때 나머지 변수에 대한 확률질량함수
- 조건부확률질량함수의 합 = 1
- \[p_{X \vert Y}(x \vert y) = {p_{XY}(x,y) \over P_Y(y)}\]
- \[p_{Y \vert X}(y \vert x) = {p_{XY}(x,y) \over P_X(x)}\]
- y=A 일 때의 결합확률질량함수의 단면
- y=A 일 때의 확률의 합
다변수 연속확률변수
- 연속확률분포에서는 이산확률분포와 같이 단순사건을 이용한 확률 정의가 불가하므로 단변수 연속확률변수같이 누적확률분포함수를 먼저 정의한 후 이를 미분하여 확률밀도함수를 정의
결합누적확률분포함수
- 연속 확률변수 X,Y에 대한 결합누적확률분포함수
- \[F_{XY}(x,y) = P({X < x} \in {Y < y}) = P({X < x, Y < y})\]
- \[F_{XY}(\infty, \infty) = 1\]
- \[F_{XY}(-\infty, y) = F{XY}(x, -\infty) = 0\]
결합확률밀도함수
- 결합확률밀도함수 (joint probability density function)
- 단변수 확률변수의 경우처럼 결합누적확률분포함수를 미분하여 정의
- 독립 변수가 2개이므로 각각에 대해 모두 편미분 (partial differentication)
- \[P_{XY} = { \partial^2 F_{XY}(x,y) \over \partial x \partial y}\]
- \[\int^{x_2}_{x1} \int^{y_2}_{y_1} p_{XY}(x,y)dxdy = P({x_1 \leq X \leq x_2, y_1 \leq Y \leq y_2})\]
- \[\int^{\infty}_{-\infty} \int^{\infty}_{-\infty} p_{XY}(x,y)dxdy = 1\]
주변확률밀도함수
- 주변확률밀도함수 (marginal probability density function)
- 결합확률밀도함수를 특정한 하나의 변수에 대해 가중평균한 값
- 결합확률밀도함수를 하나의 확률변수에 대해서만 적분하여 구함
- \[p_X(x) = \int^{\infty}_{-\infty}p_{XY}(x, y)dy\]
- \[p_Y(y) = \int^{\infty}_{-\infty}p_{XY}(x, y)dx\]
조건부확률밀도함수
- 조건부확률밀도함수 (conditional probability density function)
- 다변수 확률변수 중 하나의 값이 고정된 경우 나머지 확률변수에 대한 확률밀도함수
- \[p_{X \vert Y}(x \vert y) = {p_{XY}(x, y) \over p_Y(y)}\]
- \[p_{Y \vert X}(y \vert x) = {p_{XY}(x, y) \over p_X(x)}\]
독립과 상관
- 상관: 한 확률변수의 표본 값이 달라지면 다른 확률변수의 조건부 분포가 달라질 경우
- 독립: 두 확률변수가 상관 관계가 아닌 경우
- \[p_{XY}(x,y) = p_X(x)p_Y(y)\]
- \[p_{XYZ}(x,y,z) = p_X(x)p_Y(y)p_Z(z)\]
반복시행
- 같은 확률변수에서 복수의 표본 데이터를 취하는 경우에는 각 표본은 서로 독립인 확률변수들에서 나온 표본
- \[p(x_1, x_2, x_3, \cdots, x_N) = \prod^N_{i=1}p(x_i)\]
조건부 확률분포
- 확률변수가 다른 확률변수에 독립이면 조건부 확률 분포가 조건이 되는 확률변수의 값에 영향을 받지 않음
= 두 확률변수가 독립이면 각 확률변수의 조건부확률밀도함수는 주변확률밀도함수와 같음 - \[p_{X \vert Y} (x \vert y) = {p_{XY}(x,y) \over p_Y(y)} = {p_X(x)p_Y(y) \over p_Y(y)} =p_X(x)\]
독립 확률변수의 기댓값
- \[E[ XY ] = E[X]E[Y]\]
- \[E[ (X-\mu_X)(Y-\mu_Y) ] = 0\]
독립 확률변수의 분산
- \(Var[ X+Y ] = Var[ X ] + Var[ Y ]\) (두 확률변수는 독립)
연습문제
- 7.4.1
- 0.02
- 0
- (C, C)
- 7.4.2
- 0.08
- 0.18
- 7.4.3
- B
- C
- 7.4.4
- (70, 170)
- 70
- 60
이 글은 ‘데이터 사이언스 스쿨 수학편’을 정리한 것입니다.
질문이나 오류가 있다면 댓글 남겨주세요.