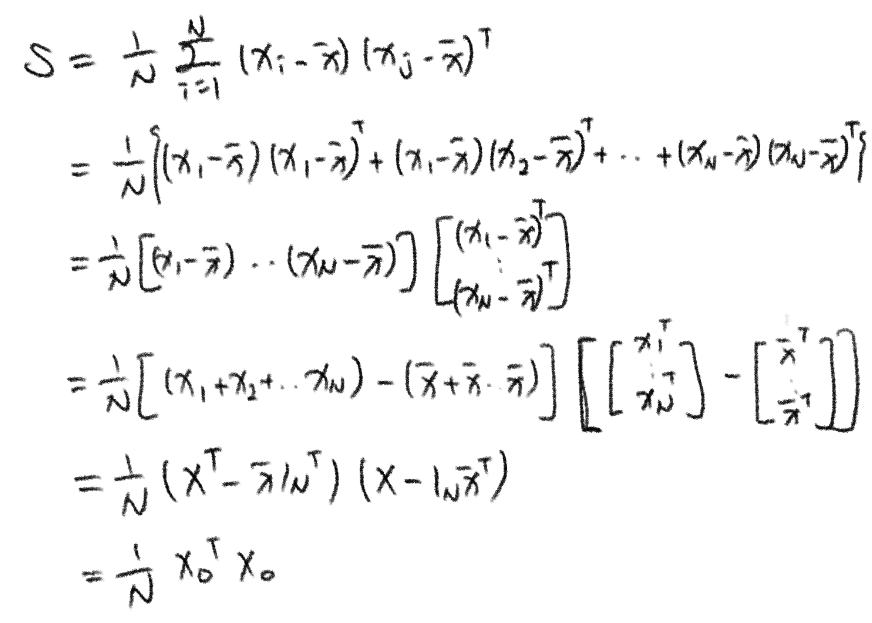표본공분산
- 표본공분산(sample covariance): 자료가 평균값으로부터 얼마나 떨어져 있는지를 나타냄
- \(s_{xy} = {1 \over N} \sum_{i=1}^N (x_i - \bar x)(y_i - \bar y)\) (\(x_i, y_i\): i번째의 x 자료와 y자료의 값, \(\bar x, \bar y\): x자료와 y자료의 표본평균)
- 평균값 위치와 표본 위치를 연결하는 사각형의 면적을 사용
- 자료의 위치에 따라 값의 부호가 달라짐
- 공분산의 부호는 데이터가 같은 부호를 가지는지 다른 부호를 가지는지에 대한 지표
표본상관계수
- 표본상관계수(sample correlation coeifficient):
- 데이터 분포의 방향성만 분리
- \(r_{xy} = {s_{xy} \over \sqrt{s_x^2 \cdot s_y^2}}\) (공분산을 각각의 표본표준편차값으로 나누어 정규화)
- 피어슨(Pearson) 상관계수라고도 함
확률변수의 공분산과 상관계수
- 공분산: \(Cov[X, Y] = E[ (X - E[X])(Y - E[Y])]\)
- 상관 계수
- \[\rho[X, Y] = {Cov[X, Y] \over \sqrt{Var[ X ] \cdot Var[ Y ]}}\]
- \[-1 \leq \rho \leq 1\]
- \(\rho = 1\): 완전선형 상관관계
- \(\rho = 0\): 무상관 (독립과는 다름)
- \(\rho = -1\): 완전선형 반상관관계
비선형 상관관계
- 비선형 상관관계: 선형이 아닌 상관관계
- 두 확률변수가 상관관계가 있으면 두 확률변수의 값 중 하나를 알았을 때 다른 확률변수의 값에 대한 정보를 알 수 있음
- 피어슨 상관계수는 두 확률변수의 관계가 선형적일 때만 상관관계를 계산
앤스콤 데이터
- 상관계수로 분포의 형상을 추측할 때 개별 자료가 상관계수에 미치는 영향력이 각각 다름
- 상관계수는 비선형 상관관계를 표현하지 못함
- 하나의 특이값(outlier) 자료에 의해 상관계수가 크게 달라질 수 있음
다변수 확률변수의 표본공분산
- 표본공분산행렬 (Sample Covariance Matrix)
- \[S = \begin{bmatrix} s_{x_1}^2 & s_{x_1x_2} & \cdots & s_{x_1x_M} \\ s_{x_1x_2} & s_{x_2}^2 & \cdots & s_{x_2x_M} \\ \vdots & \;\; \vdots& \ddots & \vdots \\ s_{x_1x_M} & s_{x_2x_M} & \cdots & s_{x_M}^2 \\ \end{bmatrix}\]
- 행렬 값을 구하는 방식
- 각 확률변수의 표본평균을 계산
- \[\bar x_j = {1 \over N} \sum^N_{i=1} x_{i,j}\]
- 각 확률변수의 분산을 계산
- \[s^2_j = {1 \over N} \sum^N_{i=1} (x_{i,j} - \bar x_j)^2\]
- 두 확률변수의 공분산을 계산
- \(s_{j,k} = {1 \over N} \sum^N_{i=1} (x_{i,j} - \bar x_j)(x_{i,k} - \bar x_k)\) - M-차원 표본 벡터로 정의하면
- \[S = {1 \over N} \sum^N_{i=1} (x_i - \bar x)(x_i - \bar x)^T\]
- 각 확률변수의 표본평균을 계산
다변수 확률변수의 공분산
- M개의 다변수 확률변수 벡터
- \[X = \begin{bmatrix} X_1 \\ X_2 \\ \vdots \\ X_M \end{bmatrix}\]
- 이론적 공분산행렬
- \[\sum = Cov[ X ] = \begin{bmatrix} \sigma^2_{x_1} & \sigma_{x_1x_2} & \sigma_{x_1x_3} & \cdots & \sigma_{x_1x_M}\\ X_2 \\ \sigma^2_{x_1x_2} & \sigma^2_{x_2} & \sigma_{x_2x_3} & \cdots & \sigma_{x_2x_M}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ \sigma^2_{x_1} & \sigma_{x_1x_2} & \sigma_{x_1x_3} & \cdots & \sigma_{x_1x_M}\\ \sigma^2_{x_1x_M} & \sigma_{x_2x_M} & \sigma_{x_3x_M} & \cdots & \sigma^2_{x_M} \end{bmatrix}\]
- \(\sigma_{x_nx_m} = (X_N-E[ X_N ])(X_M - E[X_M])\) 이므로
- \[\sum = E[ (X-E[X])(X-E[X])^T ]\]
연습문제
- 7.5.1
-
from sklearn.datasets import load_iris import scipy as sp X = load_iris().data x1 = X[:, 0] # 꽃받침의 길이 x2 = X[:, 1] # 꽃받침의 폭 x3 = X[:, 2] # 꽃잎의 길이 x4 = X[:, 3] # 꽃잎의 폭 sp.stats.pearsonr(x1, x2)[0] # -0.11756978413300206 -
sp.stats.pearsonr(x3, x4)[0] # 0.9628654314027961 -
sp.stats.pearsonr(x2, x4)[0] # -0.36612593253643905
-
- 7.5.2
-
import numpy as np np.random.seed(10) x1 = np.random.normal(size=10) np.random.seed(17) x2 = np.random.normal(size=10) sp.stats.pearsonr(x1, x2)[0] # -0.3760942268214469 -
np.random.seed(10) x1 = np.random.normal(size=10000) np.random.seed(17) x2 = np.random.normal(size=10000) sp.stats.pearsonr(x1, x2)[0] # 0.014360789995010345 - 표본상관계수는 유한한 원소를 가지고 있으므로 무한한 원소를 가진 이론적 상관계수와는 다를 수 있음
-
- 7.5.3
- 7.5.4
N,M = X.shape xbar = 1 / N * X.T @ np.ones((N,1)) xzero = X - (np.ones((N,1)) @ xbar.T) S = 1 / N * (xzero.T @ xzero) S # array([[ 0.68112222, -0.04215111, 1.26582 , 0.51282889], # [-0.04215111, 0.18871289, -0.32745867, -0.12082844], # [ 1.26582 , -0.32745867, 3.09550267, 1.286972 ], # [ 0.51282889, -0.12082844, 1.286972 , 0.57713289]])
이 글은 ‘데이터 사이언스 스쿨 수학편’을 정리한 것입니다.
질문이나 오류가 있다면 댓글 남겨주세요.