Abstract
Introduction
deep convolution networks에서 사용할 수 있는 training set 크기와 network의 크기에 대한 제한이 해결되면서 network가 점점 더 커지고 깊이졌고, deep convolution networks은 visual recognition에서 뛰어난 성능을 발휘하게 되었다.
Hence, Ciresan et al. [1] trained a network in a sliding-window setup to predict the class label of each pixel by providing a local region (patch) around that pixel as input.
convolutional network은 주로 한 개의 클래스로 결정되는 분류 문제에 사용되었다. 하지만 많은 visual 문제, 특히 의공학 이미지 처리에서 localization이 필요했다. 또한 보통 의공학 문제에서는 많은 학습 이미지를 얻기 어려웠다. 첫번째, 이 네트워크는 localization을 할 수 있다. 둘째, 패치 측면에서 학습 데이터가 학습 이미지 수보다 훨씬 많습니다. 논문에서 제안한 네트워크는 ISBI 2012의 EM segmentation challenge를 큰 차이로 우승을 차지했습니다.
Obviously, the strategy in Ciresan et al. [1] has two drawbacks. First, it is quite slow because the network must be run separately for each patch, and there is a lot of redundancy due to overlapping patches. Secondly, there is a trade-off between localization accuracy and the use of context. Larger patches require more max-pooling layers that reduce the localization accuracy, while small patches allow the network to see only little context. More recent approaches [11,4] proposed a classifier output that takes into account the features from multiple layers. Good localization and the use of context are possible at the same time.
In this paper, we build upon a more elegant architecture, the so-called “fully convolutional network” [9]. We modify and extend this architecture such that it works with very few training images and yields more precise segmentations; see Figure 1. The main idea in [9] is to supplement a usual contracting network by successive layers, where pooling operators are replaced by upsampling operators. Hence, these layers increase the resolution of the output. In order to localize, high resolution features from the contracting path are combined with the upsampled output. A successive convolution layer can then learn to assemble a more precise output based on this information.
One important modification in our architecture is that in the upsampling part we have also a large number of feature channels, which allow the network to propagate context information to higher resolution layers. As a consequence, the expansive path is more or less symmetric to the contracting path, and yields a u-shaped architecture. The network does not have any fully connected layers and only uses the valid part of each convolution, i.e., the segmentation map only contains the pixels, for which the full context is available in the input image. This strategy allows the seamless segmentation of arbitrarily large images by an overlap-tile strategy (see Figure 2). To predict the pixels in the border region of the image, the missing context is extrapolated by mirroring the input image. This tiling strategy is important to apply the network to large images, since otherwise the resolution would be limited by the GPU memory.
As for our tasks there is very little training data available, we use excessive data augmentation by applying elastic deformations to the available training im- ages. This allows the network to learn invariance to such deformations, without the need to see these transformations in the annotated image corpus. This is particularly important in biomedical segmentation, since deformation used to be the most common variation in tissue and realistic deformations can be simu- lated efficiently. The value of data augmentation for learning invariance has been shown in Dosovitskiy et al. [2] in the scope of unsupervised feature learning.
Another challenge in many cell segmentation tasks is the separation of touch- ing objects of the same class; see Figure 3. To this end, we propose the use of a weighted loss, where the separating background labels between touching cells obtain a large weight in the loss function.
The resulting network is applicable to various biomedical segmentation prob- lems. In this paper, we show results on the segmentation of neuronal structures in EM stacks (an ongoing competition started at ISBI 2012), where we outperformed the network of Ciresan et al. [1]. Furthermore, we show results for cell segmentation in light microscopy images from the ISBI cell tracking chal- lenge 2015. Here we won with a large margin on the two most challenging 2D transmitted light datasets.
Network Architecture
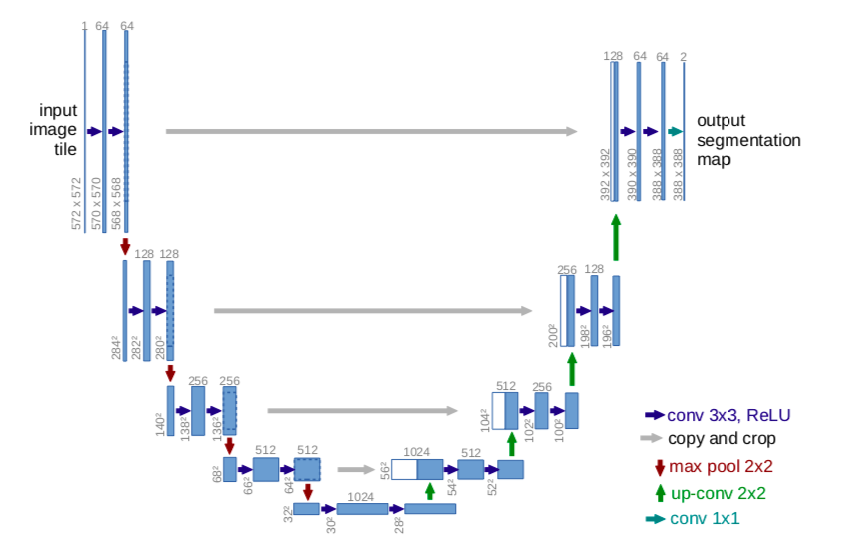
- The network structure is as above. It consists of a contraction path (left) and an extension path (right). The contraction path follows the general structure of the convolutional network. There are two 3x3 convolution (convolution without padding), each convolution with a stride of 2 for downsampling and ReLU. For each downsampling, the number of feature channels was doubled. All steps in the extension path consist of 2x2 convolution (“up-convolution”) that halves the number of feature channels following upsampling of feature maps. This is connected to the corresponding cropped feature map in the contraction path, followed by two 3x3 convolution, ReLU. Cropping is required because pixels on the border are lost in all convolutions. In the last layer, the 1x1 convolution is used to map 64 configuration feature vectors to the desired number of classes. There are a total of 23 convolutional layers in this network.
- 네트워크 구조는 위와 같다. 수축 경로(왼쪽)와 확장 경로(오른쪽)로 구성됩니다. 수축 경로는 컨볼루션 네트워크의 일반적인 구조를 따릅니다. 2개의 3x3 컨볼루션(패딩이 없는 컨볼루션)이 연속적으로 있는데, 각 컨볼루션은 ReLU와 다운샘플링을 위해 스트라이드가 2인 2x2 max pooling 작업이 이어집니다. 각 downsampling마다 feature 채널 수를 두배로 늘렸다. 확장 경로에서 모든 단계는 feature 맵의 upsampling에 이어 feauture 채널 수를 절반으로 줄이는 2x2 컨볼루션(“up-convolution”)으로 구성된다. 이것은 수축 경로에서 대응되는 잘라낸 feature 맵과 연결되고, 2개의 3x3 컨볼루션, ReLU이 이어진다. 모든 컨볼루션에서 테두리에 있는 픽셀이 손실되므로 cropping은 필요하다. 마지막 레이어에서 1x1 컨볼루션은 64개의 구성 feature 벡터를 원하는 클래스 수에 매핑하는 데 사용된다. 이 네트워크에는 총 23개의 컨볼루션 계층이 있다.
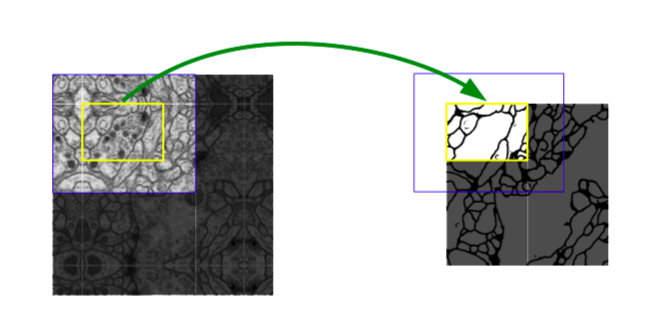
- For the smooth tiling of the final segmentation map, it is important to select an input tile size such that all 2x2 max pooling operations make x and y sizes even in the layer
- 최종 segmentation 맵의 원활한 타일링을 위해 모든 2x2 max pooling 연산이 레이어에서 x와 y 크기가 짝수가 되도록 하는 입력 tile 크기를 선택하는 것이 중요하다.
Training
Data Augmentation
Experiments
Conclusion
This is written by me after review a paper.
If you have questions, you can leave a reply on this post.