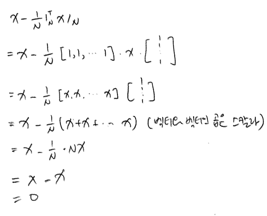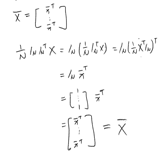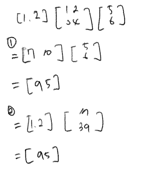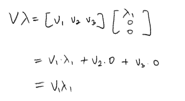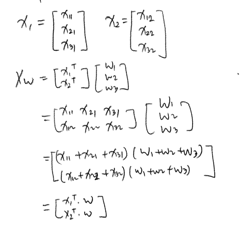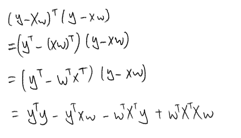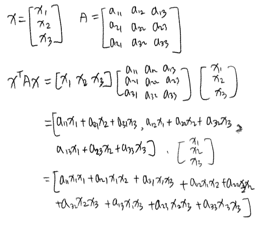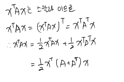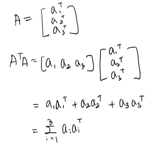벡터/행렬의 덧셈과 뺄셈

:요소별 연산(element-wise): 크기가 같은 두 벡터와 행렬에서 같은 위치의 원소끼리 연산을 하는 것

\(x = \begin{bmatrix}10\\11\\12\end{bmatrix}, y = \begin{bmatrix}1\\2\\3\end{bmatrix}\)
\(x + y = \begin{bmatrix}11\\13\\15\end{bmatrix}, x - y = \begin{bmatrix}9\\9\\9\end{bmatrix}\)

x = np.array([10, 11, 12])
y = np.array([1, 2, 3])
print(x + y)
print(x - y)
>>>
array([11, 13, 15])
array([9, 9, 9])

스칼라와 벡터/행렬의 곱셈

스칼라와 벡터/행렬의 곱셈은 벡터/행렬의 각 원소에 스칼라값을 곱하는 것과 같다

\(c \begin{bmatrix}x_1\\x_2\end{bmatrix} = \begin{bmatrix}cx_1\\cx_2\end{bmatrix}\)

브로드캐스팅

벡터와 스칼라의 덧셈/뺄셈의 경우 1-벡터를 이용하여 스칼라를 벡터로 변환 뒤 연산을 할 수 있다

\(\begin{bmatrix}11\\12\\13\end{bmatrix} - 10 = \begin{bmatrix}11\\12\\13\end{bmatrix} - 10 \cdot 1 = \begin{bmatrix}11\\12\\13\end{bmatrix} - \begin{bmatrix}10\\10\\10\end{bmatrix}\)

선형조합

:벡터/행렬에 스칼라값을 곱한 후 더하거나 뺀 것
선형조합 이후에도 벡터/행렬의 크기는 변하지 않는다
\(c_1x_1 + c_2x_2 + \cdots + c_Lx_L = x\)
\(c_1A_1 + c_2A_2 + \cdots + c_LA_L = x\)
\((c_i \in R, x_i \in R^M, A_i \in R^{M \times N})\)

벡터와 벡터의 곱셈

내적(dot product): \(x \cdot y = <x, y> = x^Ty\) (스칼라 값이 된다)
내적 조건

  1. 두 벡터의 차원(길이)이 같아야 한다.
  2. 앞은 행벡터, 뒤는 열벡터이여야 한다. \(x^Ty = \begin{bmatrix}x_1 && x_2 && \cdots && x_N\end{bmatrix}\begin{bmatrix}y_1\\y_2\\\vdots\\y_N\end{bmatrix} = x_1y_1 + \cdots + x_Ny_N = \sum_{i=1}^N x_iy_i\)
    \((x \in R^{N \times 1}, y \in R^{N \times 1}, x^Ty \in R)\) 
    x = np.array([[10], [11], [12]])
y = np.array([[1], [2], [3]])
z = np.array([10, 11, 12])
k = np.array([1, 2, 3])
print(x.T @ y)
print(x @ y) # 넘파이에서는 1차원 배열의 내적도 가능
>>>
array([[58]])
58

가중합

: 여러 개의 원소가 있을 때 각각 특정 가중치를 곱한 후의 곱셈 결과들을 합한 것
벡터의 내적을 이용하여 계산

가중평균

: 가중합의 가중치값을 전체 가중치값의 합으로 나눈 것 (\(\bar{x}\))
ex) 수학: (100점, 가중치3), 영어: (60점, 가중치1)
\(\frac{3}{3+1} \times 100 + \frac{1}{3+1} \times 60 = 90\)

유사도

: 두 벡터의 닮은 정도를 정량적으로 나타낸 값
두 벡터가 비슷할수록 유사도가 커진다
코사인 유사도: 내적을 이용하여 유사도 계산

선형회귀 모형

: 독립변수들을 통해 종속변수를 예측하는 방법 (단, 비선형적인 데이터로는 현실 세계의 데이터 예측 성능이 떨어진다)
\(\hat y = w_1x_1 + \cdots + w_Nx_N\) ( \(\hat y\): 예측값, \(w\): 가중치 벡터, \(x\): 독립벡터)
\(\hat y = w^Tx\)

제곱합

: 벡터의 각 원소를 제곱한 뒤에 더한 것
분산이나 표준 편차 계산에 사용
\(x^Tx = \begin{bmatrix}x_1 && x_2 && \cdots && x_N\end{bmatrix} \begin{bmatrix}x_1\\x_2\\\vdots\\x_N\end{bmatrix} = \sum_{i=1}^N x_i^2\)

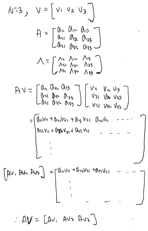
행렬과 행렬의 곱셈

\(A \in R^{N \times L}, B \in R^{L \times M} \rightarrow AB \in R^{N \times M}\)

\(\begin{bmatrix}a_{11} && a_{12} && a_{13}\\a_{21} && a_{22} && a_{23}\\a_{31} && a_{32} && a_{33}\\a_{41} && a_{42} && a_{43}\end{bmatrix} \begin{bmatrix}b_{11} && b_{12}\\b_{21} && a_{22} \\b_{31} && b_{32}\end{bmatrix} = \begin{bmatrix}a_{11}b_{11}+a_{12}b_{21} + a_{13}b_{31} && a_{11}b_{12}+a_{12}b_{22}+a_{13}b_{32}\\a_{11}b_{11}+a_{12}b_{21} + a_{13}b_{31} && a_{21}b_{12}+a_{22}b_{22}+a_{23}b_{32}\\a_{21}b_{11}+a_{22}b_{21} + a_{33}b_{31} && a_{31}b_{12}+a_{32}b_{22}+a_{33}b_{32}\\a_{41}b_{11}+a_{42}b_{21} + a_{43}b_{31} && a_{41}b_{12}+a_{42}b_{22}+a_{43}b_{32}\end{bmatrix}\)

A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.array([[1, 2], [3, 4], [5, 6]])
A @ B
>>>
array([[22, 28],
       [49, 64]])
58

: 행렬의 곱셈은 임의의 순서로 해도 똑같다
\(ABC = (AB)C = A(BC)\)
항등행렬과의 곱은 언제나 자기 자신이 된다
\(AI = IA = A\)

교환 법칙과 분배 법칙

행렬 \(A, B\) 에 대해
\(AB \neq BA\)
\(A(B + C) = AB + AC\)
\((A+B)C = AC + BC\)
\((A+B)^T = A^T + B^T\)
\((AB)^T = B^TA^T\)
\((ABC)^T =C^TB^TA^T\)

행렬과 벡터의 곱

: 행렬과 벡터의 곱은 행렬의 행벡터와 벡터의 선형조합을 한 벡터와 같다

\(\begin{bmatrix}x_{1,1} && x_{1,2} && \cdots && x_{1,N}\\x_{2,1} && x_{2,2} && \cdots && x_{2,N}\\ \vdots && \vdots && \vdots && \vdots\\x_{M,1} && x_{M,2} && \cdots && x_{M,N}\end{bmatrix} \begin{bmatrix}w_1 \\ w_2 \\ \vdots \\ w_N\end{bmatrix} = \begin{bmatrix}w_1x_{1,1} + w_2x_{1,2} + \cdots + w_Nx_{1,N} \\ w_1x_{2,1} + w_2x_{2,2} + \cdots + w_Nx_{2,N} \\ \vdots \\ w_1x_{M,1} + w_2x_{M,2} + \cdots + w_Nx_{M,N}\end{bmatrix}\) 즉 \(\hat y =Xw\)

잔차

: 실제값과 예측치의 차이 (=오차)
\(e_i = y_i - \hat y_i = y_i - w^Tx_i\)

\(e = \begin{bmatrix}e_1 \\ e_2 \\ \vdots \\ e_M\end{bmatrix} = \begin{bmatrix}y_1 \\ y_2 \\ \vdots \\ y_N\end{bmatrix} - \begin{bmatrix}x_1^Tw \\ x_2^Tw \\ \vdots \\ x_M^Tw\end{bmatrix} = y - Xw\)
잔차의 크기 비교는 잔차 벡터의 제곱합을 통하여 구한다
\(e^Te = (y-Xw)^T(y-Xw) = \sum_{i=1}^N e_i^2\)

이차형식

: 행벡터 \(\times\) 정방행렬 \(\times\) 열벡터의 형식으로 되어 있는 것
\(w^TX^TXw = w^TAw = \sum_{i=1}^N \sum_{j=1}^N a_{i,j}x_ix_j\)

부분행렬

: 정방행렬을 행벡터나 열벡터로 나눈 행렬이다. \(A = \begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22}\end{bmatrix} = \begin{bmatrix}a_1^T \\ a_2^T \end{bmatrix} = \begin{bmatrix} b_1 && b_2 \end{bmatrix}\)

연습문제

  • 2.2.1 
      import numpy as np
  p = np.array([[100], [80], [50]])
  n = np.array([[3], [4], [5]])
  p.T @ n
  >>>
  [[870]]
  • 2.2.2
    • 2
  • 2.2.3 
      from sklearn.datasets import load_digits
  X = load_digits().data
  x1 = X[0]
  x10 = X[9]
  x1.T @ x10
  >>>
  2807.0
    
  X @ X.T
  >>>
  array([[3070., 1866., 2264., ..., 2812., 3006., 2898.],
         [1866., 4209., 3432., ..., 3906., 3083., 3307.],
         [2264., 3432., 4388., ..., 4005., 3063., 3697.],
         ...,
         [2812., 3906., 4005., ..., 5092., 3729., 4598.],
         [3006., 3083., 3063., ..., 3729., 4316., 3850.],
         [2898., 3307., 3697., ..., 4598., 3850., 4938.]])
  • 2.2.4
    • (1)
      • 4_1 
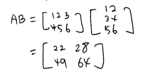
          A = np.array([[1,2,3], [4,5,6]])
  B = np.array([[1,2], [3,4], [5,6]])
  A @ B
  >>>
  array([[22, 28],
     [49, 64]])
    • (2)
      • 4_2 
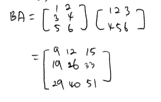
          B @ A
  >>>
  array([[ 9, 12, 15],
     [19, 26, 33],
     [29, 40, 51]])
  # A @ B 와 B @ A는 다르다
    • (3)
      • 4_3
      • 4_4 
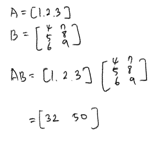
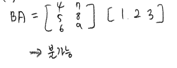
          A = np.array([1, 2, 3])
  B = np.array([[4,7], [5,8], [6,9]])
  A @ B
  >>>
  array([32, 50])
  B @ A
  # 에러 발생
  >>>
  ValueError: matmul: Input operand 1 has a mismatch in its core dimension 0, with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 3 is different from 2)
    • (4) 
        A = np.array([[1,2],[3,4]])
  B = np.array([[5,6], [7,8]])
  A @ B
  >>>
  array([[19, 22],
         [43, 50]])         
  B @ A
  >>>
  array([[23, 34],
         [31, 46]])
  # A @ B 와 B @ A는 다르다
    • (5)
      • 4_5 
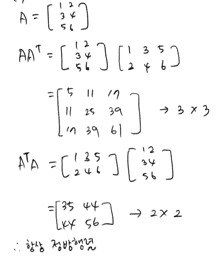
          A = np.array([[1,2], [3,4], [5,6]])
  A @ A.T
  >>>
  array([[ 5, 11, 17],
     [11, 25, 39],
     [17, 39, 61]])
  # 3x3 정방행렬
  A.T @ A
  >>>
  array([[35, 44],
     [44, 56]])
  # 2x2 정방행렬
    • (6)
      • 4_6 
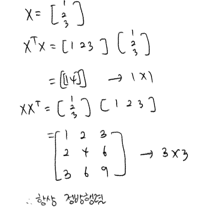
          X = np.array([[1], [2], [3]])
  X.T @ X
  >>>
  array([[14]]) # 스칼라
  X @ X.T
  >>>
  array([[1, 2, 3],
     [2, 4, 6],
     [3, 6, 9]])
  # 정방행렬
  • 2.2.5
    • (1)
      • 5_1
    • (2)
      • 5_2
    • (3)
      • 5_3
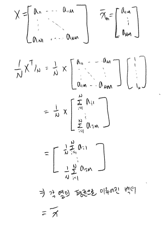
    • (4) 
        from sklearn.datasets import load_iris
  X = load_iris().data
  N = X.shape[0]
  ones = np.ones(N).reshape(-1, 1)
  ((ones @ ones.T) @ X) / N
  >>>
  array([[5.84333333, 3.05733333, 3.758     , 1.19933333],
         [5.84333333, 3.05733333, 3.758     , 1.19933333],
                    ...
         [5.84333333, 3.05733333, 3.758     , 1.19933333]])
  • 2.2.6
    • 6
  • 2.2.7
    • 7
  • 2.2.8
    • 8
  • 2.2.9
    • 9
  • 2.2.10
    • 10
  • 2.2.11
    • 11
  • 2.2.12
    • 12
  • 2.2.13
    • 13
  • 2.2.14
    • 14



이 글은 ‘데이터 사이언스 스쿨 수학편’을 정리한 것입니다. 질문이나 오류가 있다면 댓글 남겨주세요.