Image classification

  • pictures are composed of many pixels -> used for classification
  • challenges
    • viewpoint variation: pixels are different depending on the angle taken
    • illumination
    • deformation
    • occulsion
    • background cluter: things that overlap with the surroundings
    • intraclass variation
  • attempts
    • picture -> find edge -> find conrners -> recognize
      -> work well, but this process should be done for all photographs
      -> can’t use
    • Data-Driven Approach
      1. collect data
      2. use ML to train a classifer
      3. evaluate the classifier on new images
        • 1st classifier: Nearest Neighbor
          • memorize all data & labels
          • compare with all the pictures and predict the label of the most similar training image
          • distance metric: L1 distance
          • train O(1), predict O(N) per one data-> train can be slow, but predict should be fast to use
        • 2nd classifier: K-Nearest Neigthbor
          • predict by checking the nearest K data
          • Distance Metric to compare images
            • L1(Manhattan) distance \(d_1(I_1, I_2) = \sum_p(I_1^p - I_2^p)\)
              • use when vector pointers are important
              • insensitivity to Outliers
            • L2(Euclidean) distance \(d_2(I_1,I_2) = \sqrt{\sum_p(I_1^p - I_2^p)^2}\)
              • value does not change when rotating images
                -> usually used
              • sensitivity to Outliers
          • K-nearset neighbor on images never used
            1. very slow at test time
            2. distance metrics on pixels are not informative
              -> it says it’s the same even if it changes
            3. curse of dimensionality
              -> it occurs when the number of variables increases over the data, which means that the space between data increases as dimensions increase. If this happens, it can be judged that completely different data are the same.

Hyperparameter

: choices determined by the user, not by learning
ex) best value of k, best distance to use => problem-dependent

  • setting hyperparameters ideas
    1. choose hyperparameters work best on the data
      -> X (only works well with training data)
    2. split data into train and test, choose hyperparameters that work best on test data
      -> X (does not apply to new data)
    3. split data into train, validation, test
      choose hyperparameters on validation data and evalutate on test data
      -> better!
    4. cross-validation
      split data into folds, try each fold as validation and average the results
      -> useful for small datasets, not used frequently in deep learning (when there is a lot of data, the calculation and cost become too large)

Linear Classification

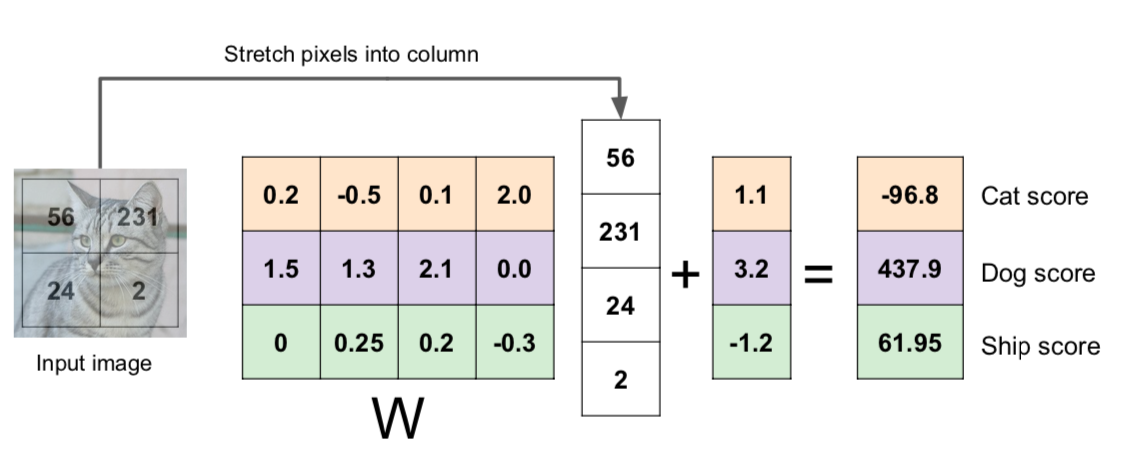
image -> \(f(x, W)\) (\(W\): weights/parameters) -> giving class scores
ex) \(f(x,W) = Wx + b\) (input: \(32\times32\times3=3072 \times 1\), \(f:10\times1\), \(w=10\times3072\), \(x=3072\times1\), \(b=10\times1\)) 1

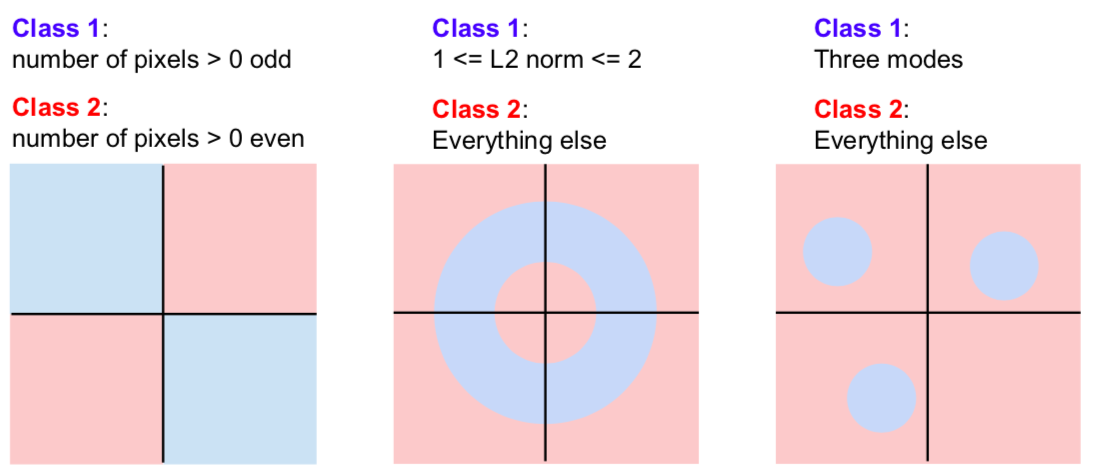
hard cases for a linear classifier 2



This is written by me after taking CS231n Spring 2017 provided by Stanford University. If you have questions, you can leave a reply on this post.