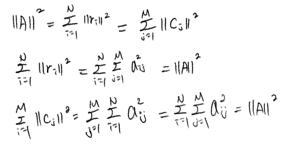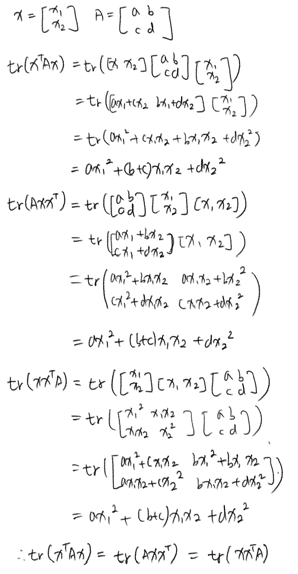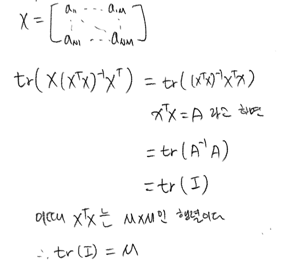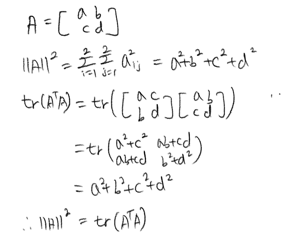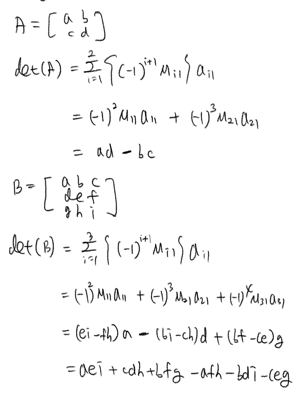정부호와 준정부호
대칭 행렬 \(A\)가 영벡터가 아닌 모든 벡터 x에 대해,
- 양의 정부호: \(x^TAx > 0\)
- 양의 준정부호: \(x^TAx \geq 0\)
\(x^TAx = \begin{bmatrix}x_1 & x_2 & x_3\end{bmatrix} \begin{bmatrix}2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2\end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}\)
\(= x_1^2 + (x_1 - x_2)^2 + (x_2 - x_3)^2 + x_3^2\) 이므로
\(x_1 = x_2 = x_3 = 0\)인 경우를 제외하고는 항상 \(0\)보다 크다
행렬 놈
-
요소별 행렬 놈(entrywise matrix norm)
\(\|A\|_p = (\sum_i^N\sum_j^M|a_{ij}|^p)^{1/p}\) -
프로베니우스 놈(Frobenius norm)
p가 2인 놈
\(\|A\| = \|A\|_2 = \|A\|_F = \sqrt{\sum_i^N\sum_j^Ma_{ij}^2}\)
놈을 최소화하는 것은 벡터의 제곱합을 최소화하는 것과 같다
\(\|x\|^2 = \sum_{i=1}^Nx_i^2 = x^Tx\) -
성질
\(\|A\| \geq 0\) (\(A\): 행렬, 영행렬일 때만 놈의 값이 0)
\(\|{\alpha A}\| = |\alpha|\|A\|\) (\(\alpha\): 스칼라)
\(\|A+B\| \leq \|A\| + \|B\|\)
\(\|AB\| \leq \|A\|\|B\|\) (A,B: 정방행렬)
대각합
-
정방행렬의 대각원소 합
\(tr(A) = a_{11} + a_{22} + \cdots + a_{NN} = \sum_{i=1}^Na_{ii}\)
음수가 될 수도 있음 -
성질 (c:스칼라, A,B,C: 행렬) \(tr(cA) = ctr(A)\)
\(tr(A^T) = tr(A)\)
\(tr(A+B) = tr(A) + tr(B)\)
\(tr(AB) = tr(BA)\)
\(tr(ABC) = tr(BCA) = tr(CAB)\) -> trace trick (아래 두 식에서는 최종값이 정방행렬이기만 하면 됨)
행렬식
-
\(det(A), det A, |A|\) (A: 정방행렬)
\(det([a]) = a\) -
스칼라가 아닐시 여인수 전개 이용 (재귀적)
\(det(A) = \sum_{i=1}^N\{(-1)^{i+j_0}M_{i,j_0\}a_{ij_0}} = \sum_{i=1}^N\{(-1)^{i_0+j}M_{i_0,j\}a_{i_0j}}\) (\(i_0, j_0\): 임의의 행/열 번호)
\(M_{i,j}\): 정방행렬 A에서 i행과 j행을 지워서 얻은 행렬의 행렬식 -
여인수
\(C_{i,j} = (-1)^{i+j}M_{i,j}\) -
det(A) = \(\sum_{i=1}^NC_{i,j_0}a_{i,j_0} = \sum_{j=1}^NC_{i_0,j}a_{i_0,j}\)
- 2 X 2 행렬의 행렬식
\(det(\begin{bmatrix}a & b \\ c & d\end{bmatrix}) = ad - bc\) -
3 X 3 행렬의 행렬식
\(det(\begin{bmatrix}a & b & c \\ d & e & f \\ g & h & i\end{bmatrix}) = aei + bfg +cdh - ceg -bdi - afh\) - 성질
\(det(A^T) = det(A)\)
\(det(I) = 1\)
\(det(AB) = det(A)det(B)\)
\(A^-1A = AA^-1 = I\)
\(det(A^-1) = \dfrac 1 {det(A)}\)
\(det(A)det(A^-1) = det(I) = I\)
연습문제
- 2.3.1
- 2.3.2
- 2.3.3
- 2.3.4
- 2.3.5
- 2.3.6
- 2.3.7
- (1)
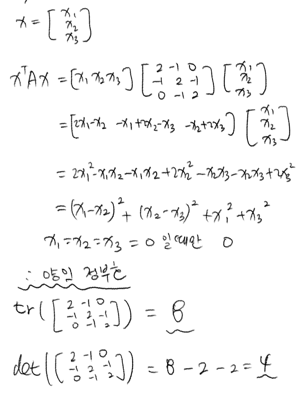
- (2)

- (1)
이 글은 ‘데이터 사이언스 스쿨 수학편’을 정리한 것입니다.
질문이나 오류가 있다면 댓글 남겨주세요.