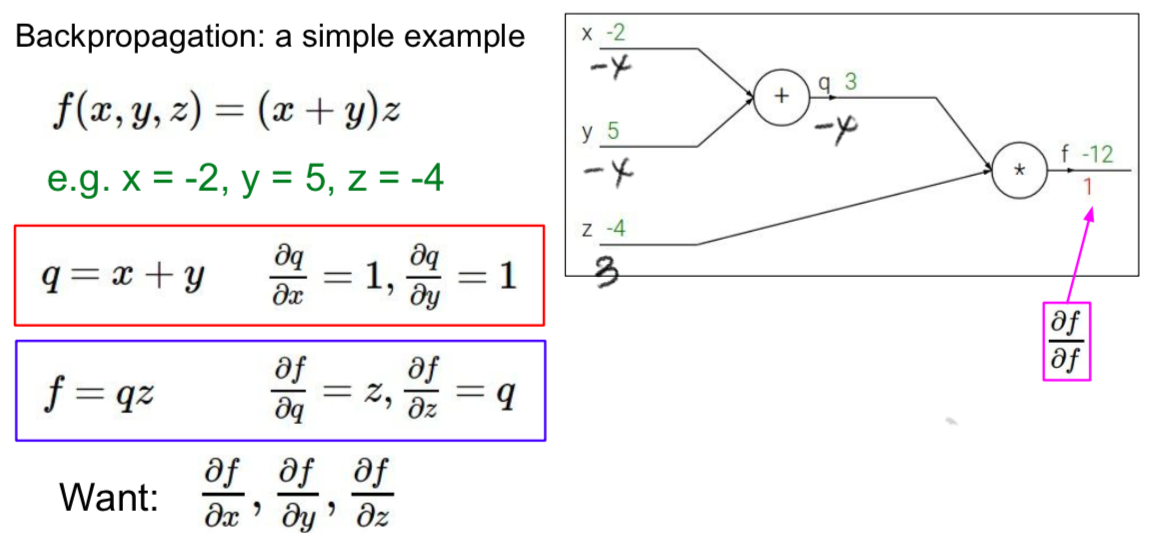
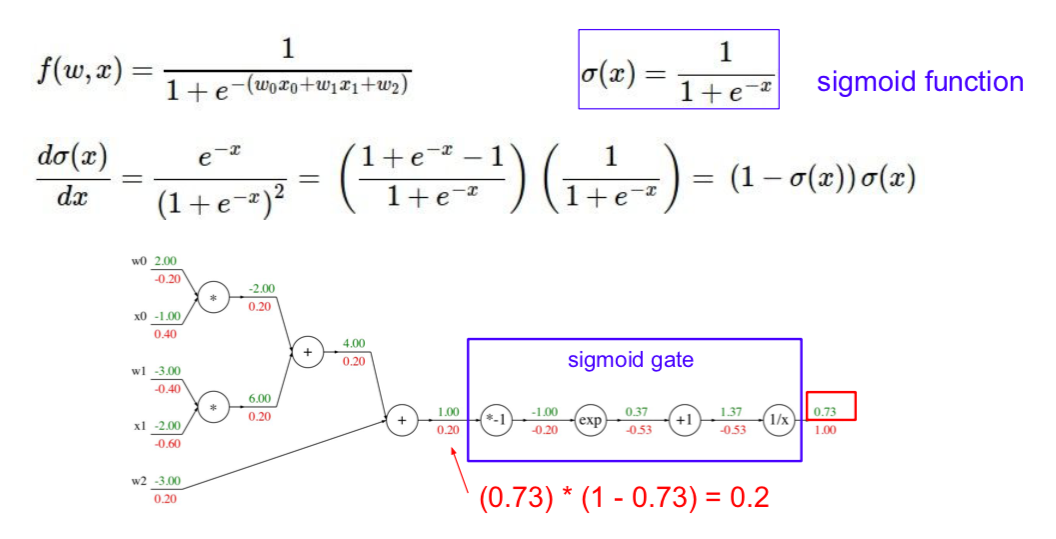
Backpropagation
- use the global gradient and local gradient to obtain all gradients

- patterns
- add gate
- gradient distributor
- send the global gradient as it is
- max gate
- gradient router
- global gradient is sent to the large value, and zero is sent to the small value
- mul gate
- gradient swithcer
- exchange each other’s values and send the values obtained by multiplying the global gradient
- add gate
- gradients add at branches
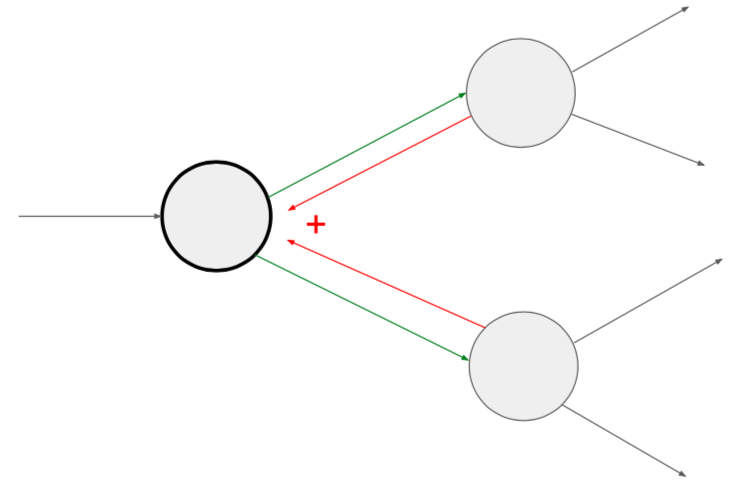
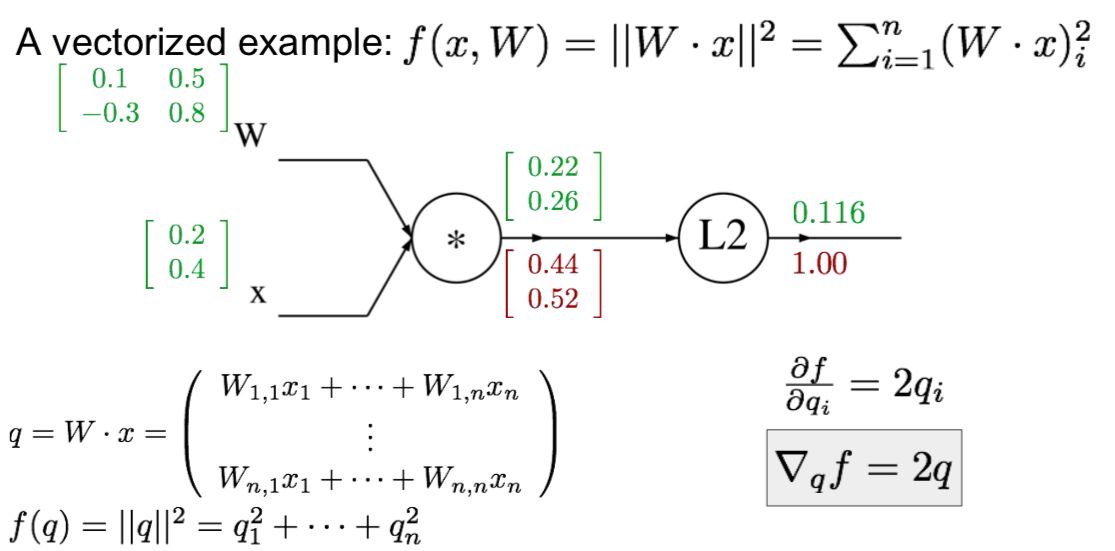
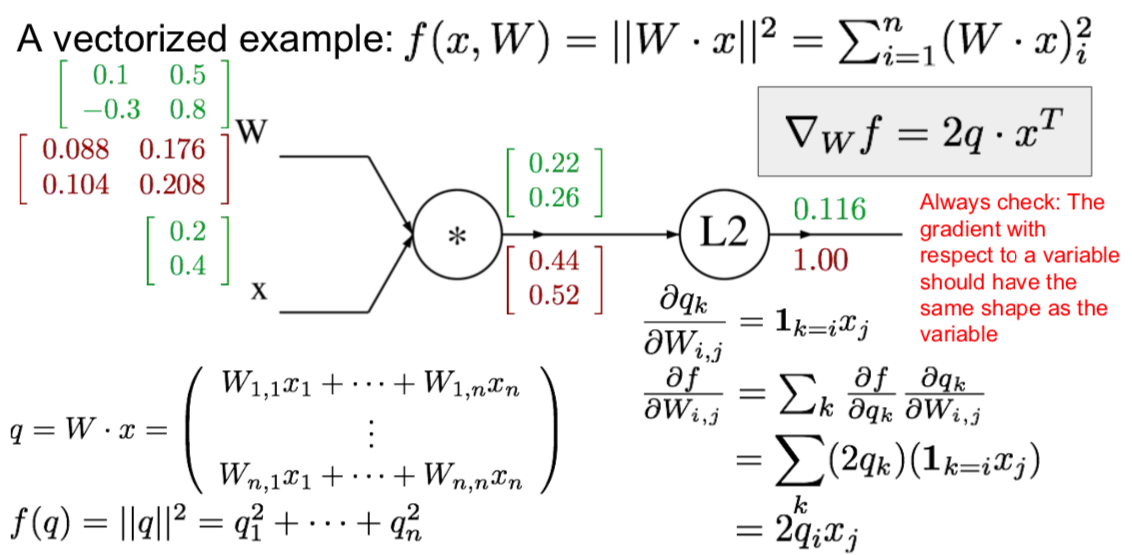
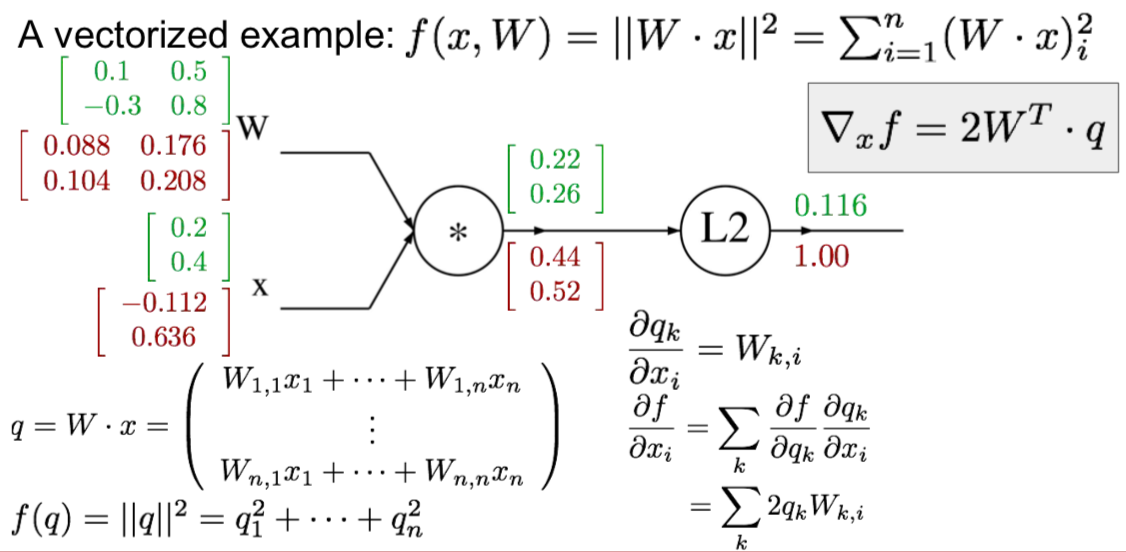
- \[{df \over dx} = \sum_i {df \over dq_i} {dq_i \over dx}\]
- vectorized operations
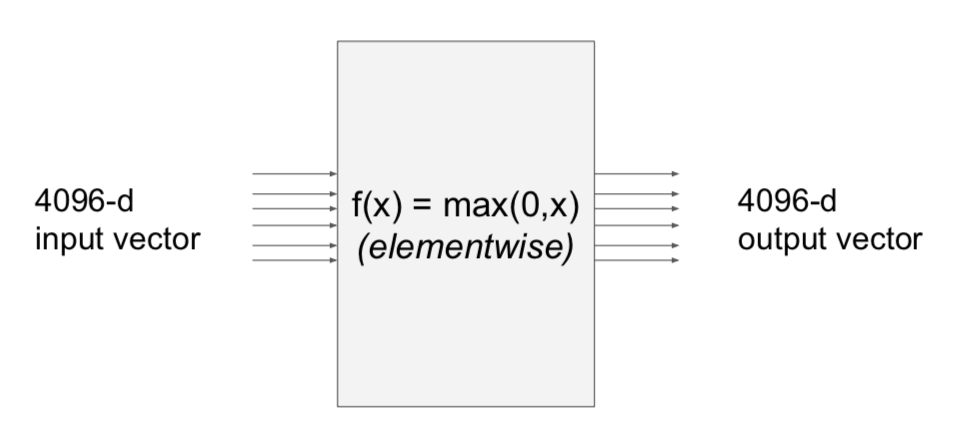
- Q. what is the size of the Jacobian matrix?
- A. 4096 x 4096
- entire minibatch (e.g. 100) of examples at one time: (409,600 x 409,600) matrix
- in practice, Jacobian Matrix is used because multivariables are processed
- vectorized example
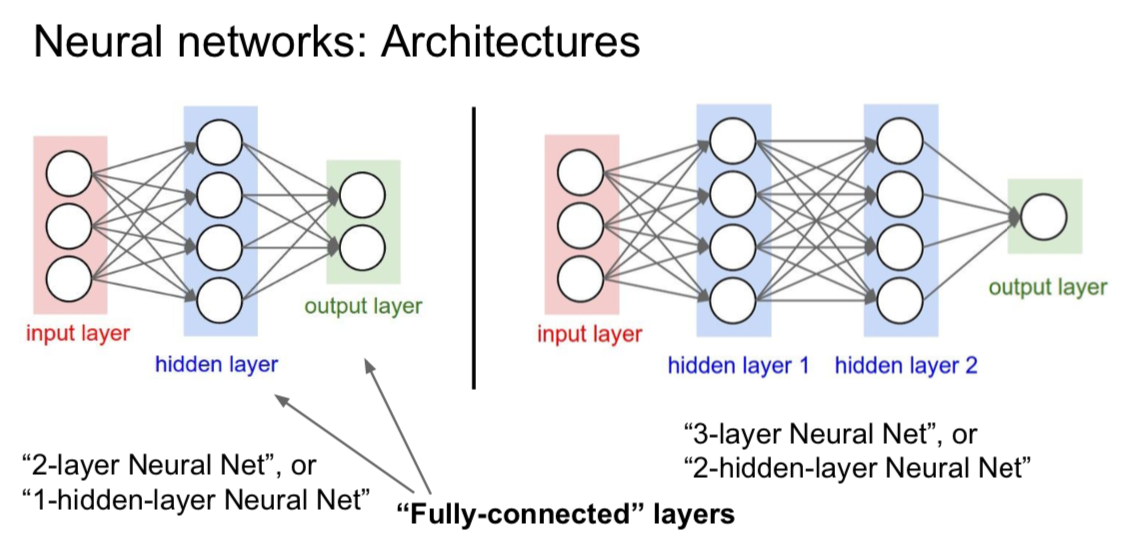
Neural Networks
- without the brain stuff
- before
- Linear score function \(f = Wx\)
- now
- 2-layer Neural Network \(f = W_2 max(0, W_1x)\)
- 3-layer Neural Network \(f = W_3 max(0, W_2 max(0, W_1x))\)
- before
- with the brain stuff
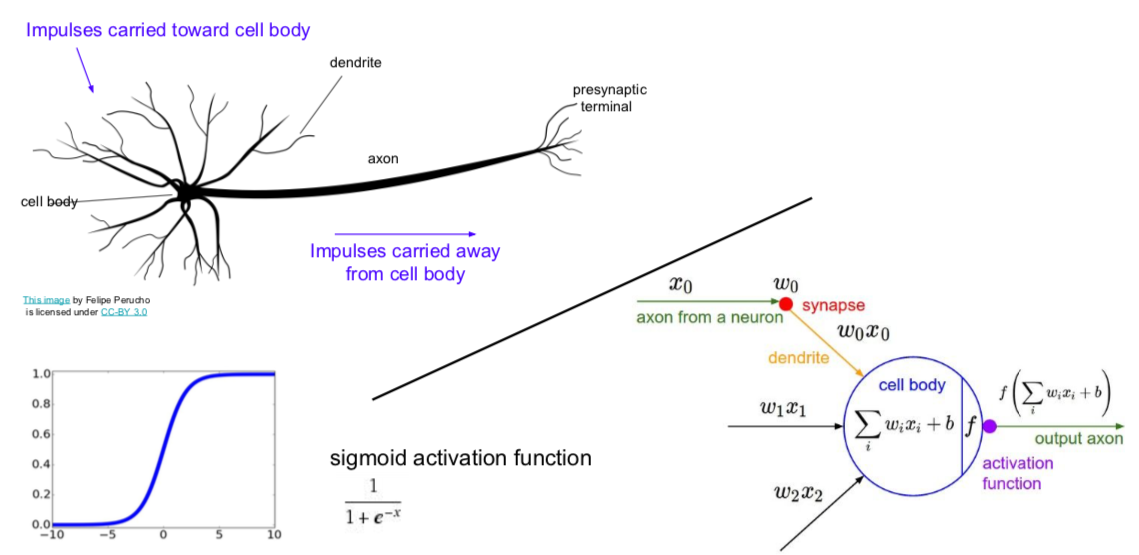
- biological neurons’ differences
- many different types
- dendrites can perform complex non-linear computations
- synapses are not a single weight but a complex non-linear dynamical system
- rate code may not be adequate
This is written by me after taking CS231n Spring 2017 provided by Stanford University.
If you have questions, you can leave a reply on this post.