Fully Connected Layer
- 32 x 32 x 3 image -> stretch to 3072 x 1 -> 10 x 3072 weights -> 1 x 10 -> activation -> 1 number
Convolution Layer
- Why is it convolutional?
- it is related to convolution of two signals
- preserve spatial structure to take advantage of the spatial features of an image
- use filters which always extend the full depth of the input volume
- ex) 32 x 32 x 3 image, 5 x 5 x 3 filter
- to calculate using filters, both a filter and a part of an image are increased to (the size of the filter) x 1, and they are calculated and bias is added. (\(w^Tx + b\))
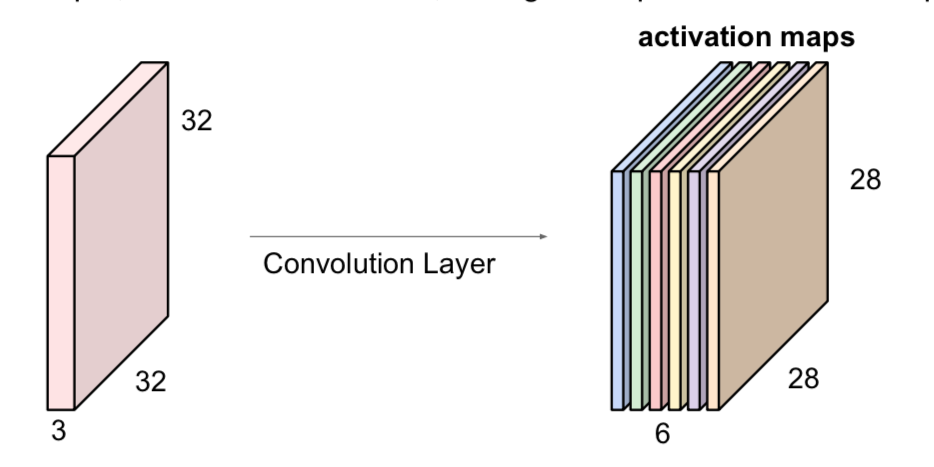
- applying multiple filters to an image stacks up activation maps (activation map is output of particular convolution layer)
- ex) 32 x 32 x 3 image, 5 x 5 x 3 filter x 3 -> 28 x 28 x 3 activation map
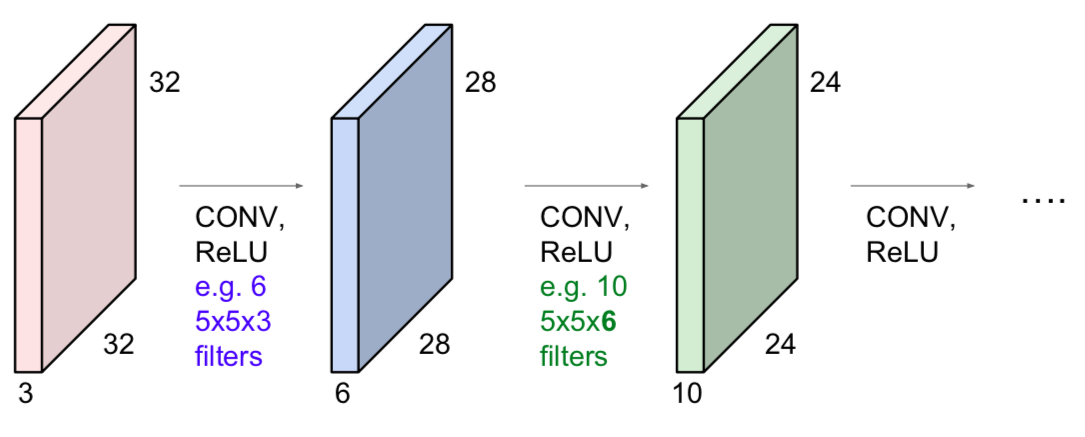
- Convnet: a sequence of Conbolution Layers, interspersed with activation functions
- Sequence: image -> Low-level features -> Mid-level features -> High-level features -> Linearly separable classifer
Filter
- stride
- 7 x 7 image + 3 x 3 filter -> 5 x 5 output
- 7 x 7 image + 3 x 3 filter + stride 2 -> 3 x 3 output
- 7 x 7 image + 3 x 3 filter + stride 3 -> Impossible (asymmetric output)
- output size: (the length of an image - the length of an filter) / stride + 1
- ex) image 7 x 7, 3 x 3 filter
- stride 1: (7-3)/1 + 1 = 5
- stride 2: (7-3)/2 + 1 = 3
- stride 3: (7-3)/3 + 1 = 2.33
- trend towards smaller filters and deeper architectures
Padding
- Why is padding used?
- to ensure that the values of the edges are also used in the same number of operations as the internal values
- to maintain the size of the input
- the size of the input is reduced quickly by using a filter, which is not good for performance
- ex) 7 x 7 image, 3 x 3 image, stride 1, pad with 1 pixel
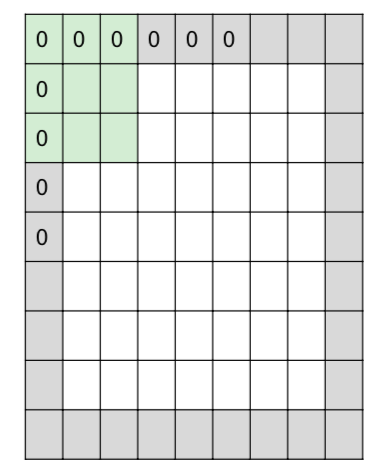
- ((7+2)-3)/1 + 1 = 7 => 7 x 7 output
- ex) 32 x 32 x 3 image, 5 x 5 filters 10, stride 1, pad 2
- in general, CONV layers with stride 1, filters of size FxF, and zero-padding with (F-1)/2
Common Settings
- number of filters K, spatial extend F, stide S, amount of zero padding P
- K: powers of 2 (32, 64, 128, …)
- F = 3, S = 1, P = 1
- F = 5, S = 1, P = 2
- F = 5, S = 2, P = whatever
- F = 1, S = 1, P = 0 -> to reduce depth while maintaining width and height of input
Brain/neuron view of CONV layer
- dot product between a part of an image and a filter = a neuron with local connectivity
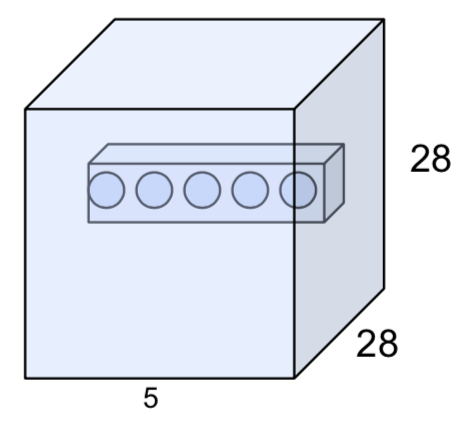
- an activation map is a (output length x output length) sheet of neuron outputs
- each is connected to a samll region in the input
- all of them share parameters (= since the same filter is used, the weight are all the same)
- ex) 32 x 32 x 3 image, 5 x 5 filters 5 -> 28 x 28 x 5
- there are 5 different neurons all looking at the same reigon in the input volume
- each neuron looks at the full input volume
Pooling
- makes the representations smaller and more manageable, but the depth is not changed (= downsampling)
- to prevent overfitting by reducing the number of parameters
- operates over each activation map independently
- Max pooling
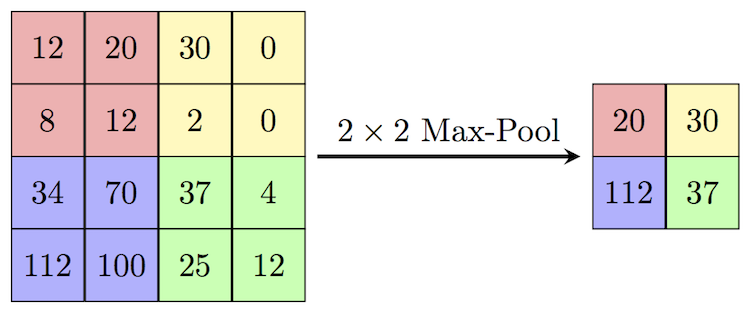
- Max pooling is better than average pooling
- because the biggest feature in that area is found
- trend towards controling stride than pooling for downsampling
- common settings
- size: 2 x 2, stride: 2
- size: 3 x 3, stride: 2
- trend towards getting rid of POOL/FC layers (just CONV)
This is written by me after taking CS231n Spring 2017 provided by Stanford University.
If you have questions, you can leave a reply on this post.

