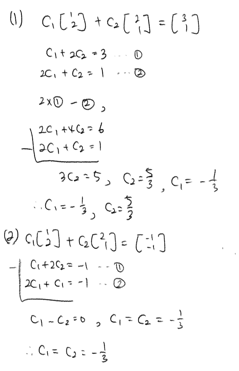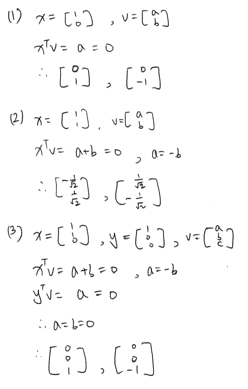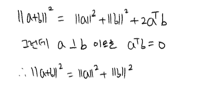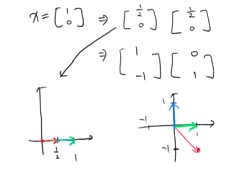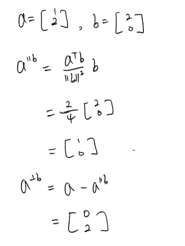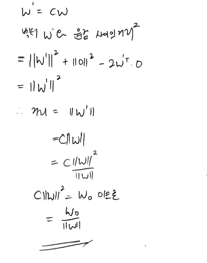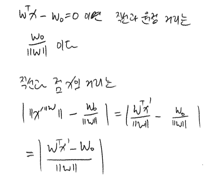벡터의 기하학적 의미
N 차원 벡터 a는 N 차원의 공간에서
- 벡터 a의 값으로 표시되는 점
- 원점과 벡터 a의 값으로 표시되는 점을 연결한 화살표(길이와 방향을 고정시킨 평행이동가능)
벡터의 길이
- 벡터 a의 길이 = \(\|a\| = \sqrt{a^Ta} = \sqrt{a_1^2 + \cdots + a_N^2}\)
스칼라와 벡터의 곱
- 양의 스칼라 x 벡터: 방향은 바뀌지 않고, 스칼라 크기만큼 벡터의 길이가 커짐
- 음의 스칼라 x 벡터: 방향이 반대가 되고, 스칼라 크기만큼 벡터의 길이가 커짐
단위벡터
- 길이가 1인 벡터 (unit vector)
- ex) \(\begin{bmatrix}1 \\ 0\end{bmatrix}, \begin{bmatrix}0 \\ 1\end{bmatrix}, \begin{bmatrix}1 \over \sqrt2 \\ 1 \over \sqrt2 \end{bmatrix}, \cdots\)
- \(x \over \|x\|\): 벡터 x가 가리키는 단위벡터 (영벡터 제외)
벡터의 합
- 두 벡터를 이웃하는 변으로 가지는 평생사변형의 대각선 벡터
- 한 벡터를 평행이동하여 다른 벡터의 끝점과 이은 벡터
벡터의 선형조합
- \(c_1x_1 + c_2x_2 + \cdots + c_Nx_N\) (\(c\): 스칼라, \(x\): 벡터)
벡터의 차
- 한 벡터가 가리키는 점으로부터 다른 벡터가 가리키는 점을 연결하는 벡터
Word2Vec
- 단어들 사이의 관계로 벡터로 표현
- ex) 일본 = 도쿄 + (한국 - 서울)
- (한국 - 서울): 서울에서 한국으로 향하는 벡터 = 수도 이름을 나라 이름으로 바꾸는 벡터
유클리드 거리
- 두 벡터가 가리키는 점 사이의 거리 (Euclidean distance)
- 유클리드 거리 = 두 벡터의 차의 길이
- \[\|a-b\| = \sqrt{\sum_{i=1}(a_i - b_i)^2} = \sqrt{\|a\|^2 + \|b\|^2 - 2a^Tb}\]
- \[\|a-b\|^2 = \|a\|^2 + \|b\|^2 - 2a^Tb\]
벡터의 내적과 삼각함수
- \[a^Tb = \|a\|\|b\|cos \theta\]
직교
- 두 벡터 a와 b가 이루는 각이 90도이면 서로 직교, \(a \bot b\)
- \[a^Tb = b^Ta = 0 \leftrightarrow a \bot b\]
정규직교
- N 개의 단위벡터 \(v_1, v_2, \cdots, v_N\)가 서로 직교할 때 (orthonormal)
- \[\|v_i\| = 1 \leftrightarrow v_i^Tv_i = 1\]
- \[v_i^Tv_J = 0 (i \neq j)\]
코사인 유사도
- 두 벡터 사이의 각의 코사인값
- 두 벡터가 같은 방향을 가리킬수록 코사인 유사도가 높아진다. (최대값 1)
- cosine similarity = \(cos \theta = {x^Ty \over \|x\|\|y\|}\)
- cosine distance = 1 - cosine similarity = \(1 - {x^Ty \over \|x\|\|y\|}\)
벡터의 분해와 성분
- 어떤 두 벡터 a, b의 합이 다른 벡터 c가 될 때, c가 두 벡터 성분 a, b로 분해된다
투영성분과 직교성분
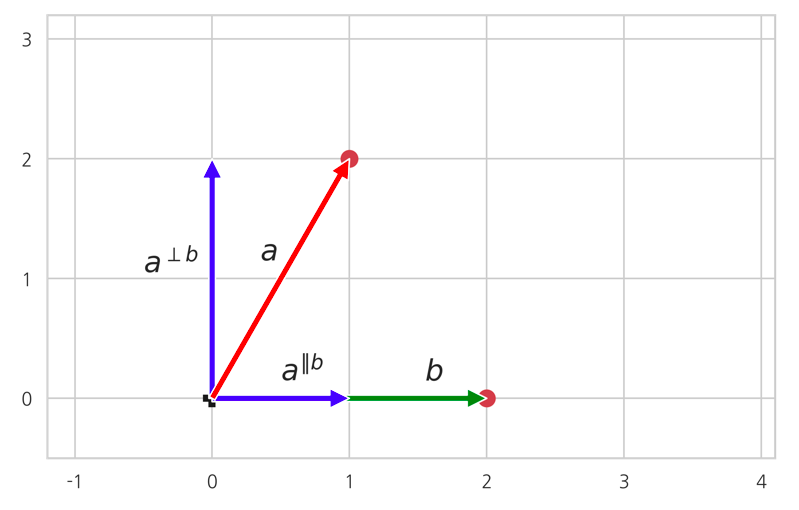
- 벡터 a를 다른 벡터 b에 직교하는 성분과 벡터 b에 평행한 성분으로 분해할 때, 평행한 선분은 벡터 b에 대한 투영성분(projection), 벡터 b에 직교하는 성분을 벡터 b에 대한 직교성분(rejection)
- Projection: \(a^{\|b}\)
- Rejection: \(a^{\bot b}\)
- 투영성분의 길이: \(\|a^{\|b}\| = \|a\|cos \theta = {\|a\|\|b\| cos \theta \over \|b\|} = {a^Tb \over \|b\|} = {b^Ta \over \|b\|} = a^T {b \over \|b\|}\)
- 벡터 b가 단위벡터라면, \(\|a^{\|b}\| = a^Tb\), \(a^{\|b} = {a^Tb \over \|b\|}{b \over \|b\|} = {a^Tb \over \|b\|^2}b, a^{\bot b} = a - a^{\|b}\)
직선의 방정식
- 어떤 벡터 w가 있을 때, 원점에서 출발한 벡터 w가 가리키는 점을 지나면서 벡터 w에 수직인 직선의 방정식
- \(w^T(x-w) = 0\) (\(x\): 위의 임의의 점을 가리키는 벡터)
- \[=> w^Tx - \|w\|^2 = 0\]
- 이 직선과 원점 사이의 거리: \(\|w\|\)
- 벡터 w에 수직인 직선의 방정식
- \(w\)와 방향이 같고 길이가 다른 벡터 \(w^\prime = cw\)을 지남
- \[w^{\prime T}x = \|w \prime \|^2 = cw^Tx - c^2\|w\|^2 = 0\]
- \(c\|w\|^2\)는 스칼라이므로, \(w^Tx - w_0 = 0\) (\(w_0\): 임의의 수)
- 이 직선과 원점 사이의 거리: \(c\|w\| = {w_0 \over \|w\|}\)
직선과 점의 거리
- 벡터 \(w\)에 대한 벡터 \(x\prime\)의 투영성분
\(\|x \prime ^{\|w}\| = {w^Tx \prime \over \|w\|}\) - 직선과 점 \(x\prime\) 사이의 거리 \(|{\|x\prime^{\|w} -\|w\|}| = |{w^Tx\prime\over\|w\|}-\|w\|| = {|w^Tx\prime - \|w\|^2 \over \|w\|} = {|w^Tx\prime - w_0| \over \|w\|}\)
연습문제
- 3.1.1
- 3.1.2
- 남자배우 = 여자배우 + (남자 - 여자)
- 3.1.3
- 3.1.4
- 3.1.5
- 3.1.6
- 3.1.7
- 3.1.8
- 3.1.9
- 3.1.10
- 3.1.11
이 글은 ‘데이터 사이언스 스쿨 수학편’을 정리한 것입니다.
질문이나 오류가 있다면 댓글 남겨주세요.