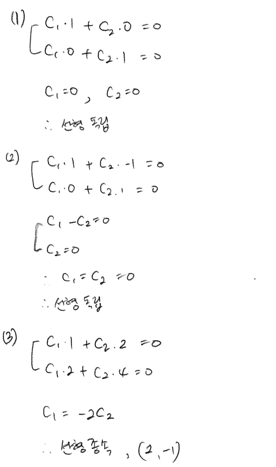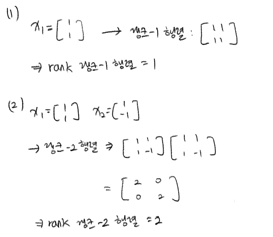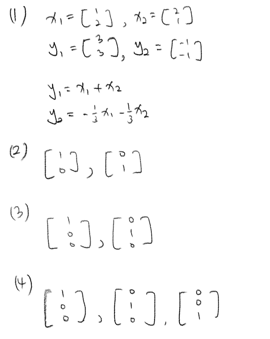선형종속과 선형독립
- 선형종속 벡터 집합 \(x_1, x_, \cdots, x_N\)에 대해 \(c_1x_1 + \cdots + c_Nx_N = 0\) 을 만족하는 스칼라 계수 \(c_1, c_2, \cdots, c_N\)가 있는 경우 (계수가 모두 0인 경우 제외)
- 선형독립 모두 0인 경우만 가능할 경우 \(c_1x_1 + \cdots + c_Nx_N = 0 \leftrightarrow c_1 = \cdots = c_N = 0\)
선형독립과 선형 연립방정식
- \[c_1x_1 + \cdots + c_Nx_N = \begin{bmatrix} x_1 & x_2 & \cdots & x_N\end{bmatrix} \begin{bmatrix}c_1 \\ c_2 \\ \vdots \\ c_N\end{bmatrix} = X_c\]
- 선형독립 판단 \(X_c = 0\)인 선형 연립방정식을 푸는 것과 같다
- 선형종속
- 영벡터가 아닌 해가 존재하는 경우 (해가 무수히 많은 경우 포함)
- 선형독립
- 해가 영벡터 밖에 없는 경우
- \(X_c = 0 \rightarrow c = 0\)
(\(X_c = 0 \leftrightarrow c = 0\))
선형종속인 경우
-
- 벡터의 개수가 벡터의 차원보다 큰 경우
- 벡터의 차원보다 벡터의 수가 많으면 미지수의 수가 방정식의 수보다 커서 해가 무수히 많다.
- 실수배의 벡터가 있는 경우
- 벡터 \(x_i\)와 \(x_j\)가 같거나 실수배일 때
\(c_j = -c_i\)라고 하고, 다른 \(c\)는 모두 0으로 한다면, \(0 \centerdot x_1 + \cdots + c_I \centerdot x_I + \cdots + c_j \centerdot x_j + \cdots + 0 \centerdot x_N\) \(= 0 \centerdot x_1 + \cdots + c_i \centerdot x_I + \cdots + (-c_i) \centerdot x_j + \cdots + 0 \centerdot x_N\) \(= 0\)
- 벡터 \(x_i\)와 \(x_j\)가 같거나 실수배일 때
- 어떤 벡터가 다른 벡터의 선형조합인 경우 \(x_1 = 2x_2 - 3x_3\)인 경우, \(-1 \centerdot x_1 + 2x_2 - 3x_3 = 0\)이므로 선형종속이다.
랭크
- 열랭크(column rank): 행렬의 열벡터 중 서로 독립인 열벡터의 최대 갯수
- 행랭크(row rank): 행렬의 행벡터 중 서로 독립인 행벡터의 최대 갯수
- 행랭크와 열랭크는 항상 같다 (행 랭크와 열 랭크를 랭크라고 하기도 함)
- \[rank \ A\]
- \[A \in R^{N \times M} \rightarrow rank \ A \leq min(M, N)\]
풀랭크
- 랭크가 행의 갯수와 열의 갯수 중 작은 값과 같은 경우
- \[rank \ A = min(M, N)\]
- 선형독립인 벡터들을 행 또는 열로 가지는 행렬을 만들면 정의에 의해 항상 풀랭크
로우-랭크 행렬
- 랭크-1 행렬(rank-1 matrix)
- N 차원 벡터 x 하나를 이용하여 만들어지는 행렬
- \[xx^T \in R^{N \times N}\]
- 열벡터들은 하나의 벡터를 \(x_1, x_2, \cdots, x_n\)배한 벡터이므로 랭크는 1
\(xx^T = x [x_1 \ x_2 \ \cdots \ x_n] = [x_1x \ x_2x \ \cdots \ x_nX]\)
- 랭크-2 행렬(rank-2 matrix)
- 선형독립인 두 개의 N차원 벡터 \(x_1, x_2\)를 이용하여 만든 행렬
- \[[x_1 \ x_2] \begin{bmatrix}x_1^T \\ x_2^T\end{bmatrix}= x_1x_1^T + x_2x_2^T\]
- 랭크 = 2
- 랭크-M 행렬(rank-M matrix)
- M개의 N차원 벡터 \(x_1, x_2, \cdots, x_M\)을 이용하여 만들어지는 행렬
- 로우-랭크 행렬(low-rank matrix)이라고 함
벡터공간과 기저벡터
- N개의 N차원 벡터가 선형독립이면 이를 선형조합하여 모든 N차원 벡터를 만들 수 있다
- 벡터공간(vector space): 서로 선형독립인 벡터들을 선형조합하여 만들어지는 모든 벡터의 집합
- 기저벡터(basis vector): 벡터공간의 벡터들
- \[V = \{ c_1x_1 + \cdots + c_Nx_N \ | \ c_1, \cdots, c_N \in R \}\]
- 벡터공간의 차원(dimension): 벡터의 차원이 아닌 기저벡터의 갯수로 정의
랭크과 역행렬
- 정방행렬이 풀랭크다 \(\leftrightarrow\) 역행렬이 존재한다
벡터공간 투영
- M개의 N차원 기저벡터 \(v_1, v_2, \cdots, v_M\)가 존재할때 (M < N),
N차원 벡터 x에 대해 기저벡터들을 조합하여 만든 벡터 \(x^{||v}\) 와 \(x - x^{||v}\) 가 모든 기저벡터에 직교하면
\(x^{||v}\) 를 벡터공간에 대한 투영벡터
\(x - x^{||v} = x^{\bot v}\) 를 벡터공간에 대한 직교벡터 - \[(x - x^{||V}) \ \bot \ \{ v_1, v_2, \cdots, v_M \}\]
정규직교인 기저벡터로 이루어진 벡터공간
- 기저벡터 \(v_1, v_2, \cdots, v_M\) 가 정규직교(orthonormal)이면
\(x^{\| V} = (x^Tv_1)v_1 + (x^Tv_2)v_2 + \cdots + (x^Tv_M)v_M\)
\(\|x^{\|V}\|^2 = \sum_{i=1}^M(x^Tv_i)^2\)
표준기저벡터
- 표준기저벡터(standard basis vector): 기저벡터 중에서 원소 중 하나만 값이 1이고 다른 값은 0으로 이루어진 기저벡터
- \[e_1 = \begin{bmatrix}1 \\ 0 \\ \vdots \\ 0\end{bmatrix}, e_2 = \begin{bmatrix}0 \\ 1 \\ \vdots \\ 0\end{bmatrix}, \cdots, e_N = \begin{bmatrix}0 \\ 0 \\ \vdots \\ 1\end{bmatrix}\]
- \[[e_1 \ e_2 \ \cdots e_N] = I_N\]
좌표
- 어떤 벡터의 좌표(coordinate): 기저벡터를 선형조합하여 그 벡터를 나타내기 위한 계수벡터
- 하나의 벡터도 기저벡터에 따라 여러 좌표를 가질 수 있음
- e.g.
기저벡터 \(\{e_1, e_2\}\) 를 선형조합하여 벡터 \(x\) 를 나타낼 수 있다면,
\(x = x_{e_1}e_1 + x_{e_2}e_2\)
\(x_e = \begin{bmatrix}x_{e_1} \\ x_{e_2}\end{bmatrix}\) : 벡터 \(x\) 의 기저벡터 \(\{ e_1, e_2 \}\) 에 대한 좌표벡터 or 좌표
\(x = [e_1 \ e_2] \begin{bmatrix}x_{e_1} \\ x_{e_2}\end{bmatrix} = [e_1 \ e_2]x_e\)
변환행렬
- 기존의 기저벡터: \(\{ e_1, e_2 \}\), 새로운 기저벡터: \(\{ g_1, g_2 \}\) 일때
\(g_1 = {1 \over \sqrt 2} e_1 + {1 \over \sqrt 2} e_2, g_2 = -{1 \over \sqrt 2} e_1 + {1 \over \sqrt 2} e_2\)
\(g_{1e} = \begin{bmatrix} {1 \over \sqrt 2} \\ {1 \over \sqrt 2}\end{bmatrix}, g_{2e} = \begin{bmatrix} -{1 \over \sqrt 2} \\ {1 \over \sqrt 2}\end{bmatrix}\)
\([g_1 \ g_2] = [e_1 \ e_2] \ [g_{1e} \ g_{2e}] = [e_1 \ e_2] A\)
\(A = \begin{bmatrix} {1 \over \sqrt 2} & -{1 \over \sqrt 2} \\ {1 \over \sqrt 2} & {1 \over \sqrt 2}\end{bmatrix}\)
좌표변환
- 좌표변환(coordinate transform): 새로운 기저벡터에 대해 좌표를 계산하는 것
- 새로운 기저벡터에 대한 좌표값이 가리키는 실제 위치는 원래의 벡터가 가리키는 실제 위치와 같아야 하므로
\(x = x_{e1}e_1 + x{e2}e_2 = x_{g1}g_1 + x_{g2}g_2\)
\(x = [e_1 \ e_2] x_e = [g_1 \ \ g_2] x_g\)
\([g_1 \ g_2] = [e_1 \ e_2] A\) 대입,
\(x = [e_1 \ e_2] x_e = [e_1 \ \ e_2] A_{x_g}\)
\(\rightarrow x_e = Ax_g, x_g = A^{-1}x_e = Tx_e\) (\(T\): 변환행렬)
연습문제
- 3.2.1
- 3.2.2
- 3.2.3
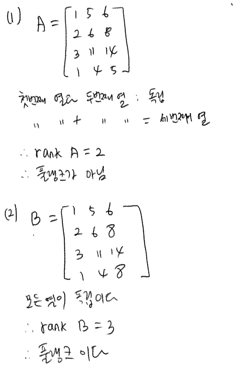
- 3.2.4
- 3.2.5
- 3.2.6
- 3.2.7
- 3.2.8
이 글은 ‘데이터 사이언스 스쿨 수학편’을 정리한 것입니다.
질문이나 오류가 있다면 댓글 남겨주세요.